| |

|
Introduction to Logic
|
Tools
for
Thought
|
|
|
Hermione Granger got it right when, facing the potion-master's test in Harry Potter, she said: "This isn't magic - it's logic - a puzzle. A lot of the greatest wizards haven't got an ounce of logic; they'd be stuck here forever."
In the real world, we are better off. We use Logic in just about everything we do. We use it in our professional lives - in proving mathematical theorems, in debugging computer programs, in medical diagnosis, and in legal reasoning. And we use it in our personal lives - in solving puzzles, in playing games, and in doing school assignments, not just in Math but also in History and English and other subjects.
Just because we use Logic does not mean we are necessarily good at it. Thinking correctly and effectively requires training in Logic, just as writing well requires training in English and composition. Without explicit training, we are likely to be unsure of our conclusions; we are prone to make mistakes; and we are apt to be fooled by others.
The ancient Greeks thought Logic sufficiently important that it was one of the three subjects in the Greek educational Trivium, along with Grammar and Rhetoric. Oddly, Logic occupies a relatively small place in the modern school curriculum. We have courses in the Sciences and various branches of Mathematics, but very few secondary schools offer courses in Logic; and it is not required in most university programs.
Given the importance of the subject, this is surprising. Calculus is important to physics. And it is widely taught at the high school level. Logic is important in all of these disciplines, and it is essential in computer science. Yet it is rarely offered as a standalone course, making it more difficult for students to succeed and get better quality jobs.
This course is a basic introduction to Logic. It is intended primarily for university students. However, it has been used by motivated secondary school students and post-graduate professionals interested in honing their logical reasoning skills.
There are just two prerequisites. The course presumes that the student understands sets and set operations, such as union, intersection, and complement. The course also presumes that the student is comfortable with symbolic mathematics, at the level of high-school algebra. Nothing else is required.
This chapter is an overview of the course. We start with a look at the essential elements of logic - logical sentences, logical entailment, and logical proofs. We then see some of the problems with the use of natural language and see how those problems can be mitigated through the use of Symbolic Logic. Finally, we discuss the automation of logical reasoning and some of the computer applications that this makes possible.
|
|
For many, Logic is an esoteric subject. It is used primarily by mathematicians in proving complicated theorems in geometry or number theory. It is all about writing formal proofs to be published in scholarly papers that have little to do with everyday life. Nothing could be further from the truth.
As an example of using Logic in everyday life, consider the interpersonal relations of a small group of friends. There are just four members - Abby, Bess, Cody, and Dana. Some of the girls like each other, but some do not.
The figure on the left below shows one set of possibilities. The checkmark in the first row here means that Abby likes Cody, while the absence of a checkmark means that Abby does not like the other girls (including herself). Bess likes Cody too. Cody likes everyone but herself. And Dana also likes the popular Cody. Of course, this is not the only possible state of affairs. The figure on the right shows another possible world. In this world, every girl likes exactly two girls, and every girl is liked by just two girls.
| |
Abby |
Bess |
Cody |
Dana |
| Abby |
|
|
 |
|
| Bess |
|
|
 |
|
| Cody |
 |
 |
|
 |
| Dana |
|
|
 |
|
|
|
| |
| |
Abby |
Bess |
Cody |
Dana |
| Abby |
 |
|
 |
|
| Bess |
|
 |
|
 |
| Cody |
 |
|
 |
|
| Dana |
|
 |
|
 |
|
|
Let's assume that we do not know the likes and dislikes of the girls ourselves but we have informants who are willing to tell us about them. Each informant knows a little about the likes and dislikes of the girls, but no one knows everything.
This is where Logic comes in. By writing logical sentences, each informant can express exactly what he or she knows - no more, no less. The following sentences are examples of different types of logical sentences. The first sentence is straightforward; it tells us directly that Dana likes Cody. The second and third sentences tell us what is not true without saying what is true. The fourth sentence says that one condition holds or another but does not say which. The fifth sentence gives a general fact about the girls Abby likes. The sixth sentence expresses a general fact about Cody's likes. The last sentence says something about everyone.
| Dana likes Cody. |
| Abby does not like Dana. |
| Dana does not like Abby. |
| Bess likes Cody or Dana. |
| Abby likes everyone that Bess likes. |
| Cody likes everyone who likes her. |
| Nobody likes herself |
Looking at the worlds above, we see that all of these sentences are true in the world on the left. By contrast, several of the sentences are false in the world on the right. Hence, we can rule out the second world.
Of course, in general, there are more than two possible worlds to consider. As it turns out, there are quite a few possibilities. Given four girls, there are sixteen possible instances of the likes relation - Abby likes Abby, Abby likes Bess, Abby likes Cody, Abby likes Dana, Bess likes Abby, and so forth. Each of these sixteen can be either true or false. There are 216 (65,536) possible combinations of these true-false possibilities, and so there are 216 possible worlds.

Logical sentences like the ones above constrain the possible ways the world could be. Each sentence divides the set of possible worlds into two subsets, those in which the sentence is true and those in which the sentence is false, as suggested by the following figure. Believing a sentence is tantamount to believing that the world is in the first set.
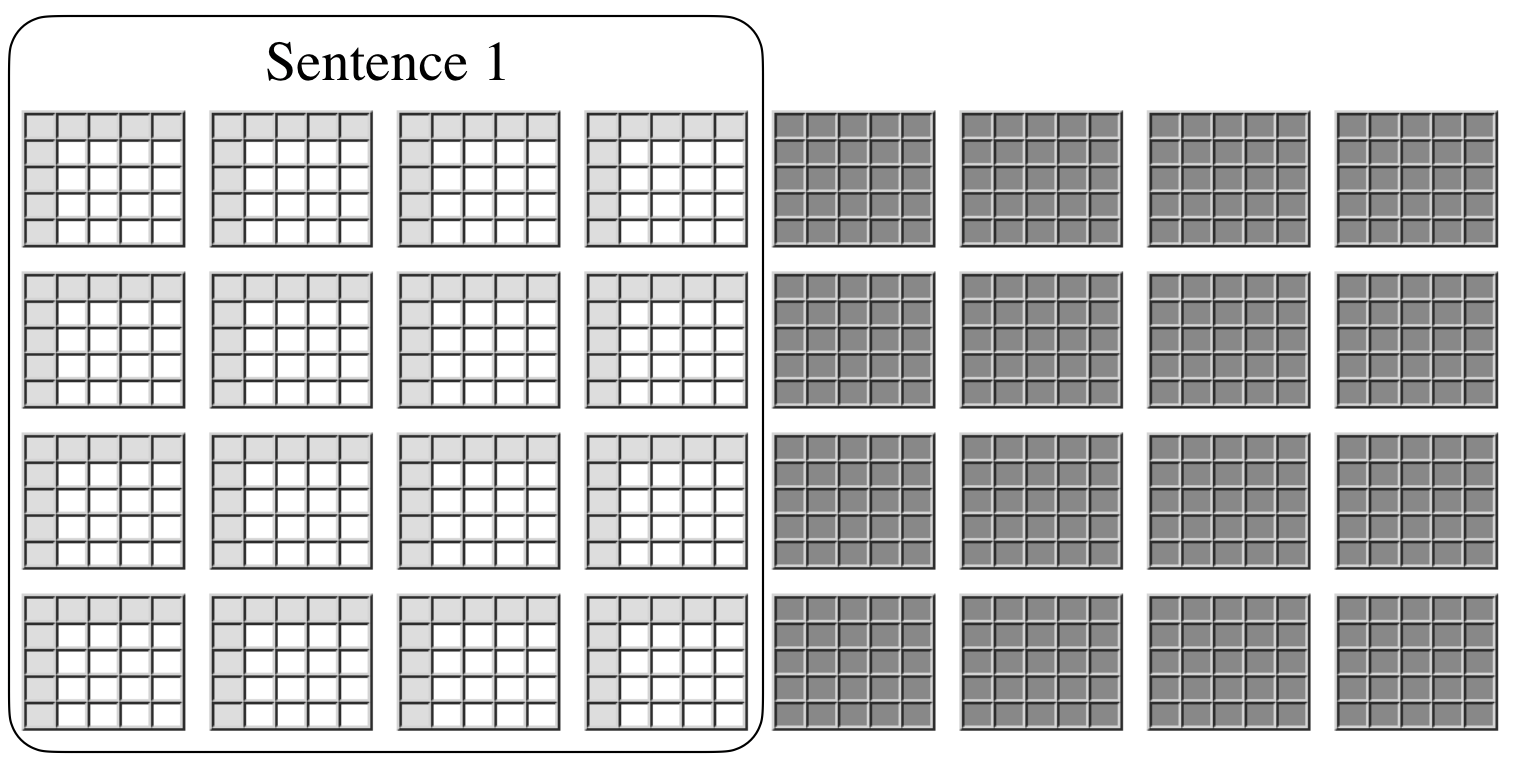
Given two sentences, we know the world must be in the intersection of the set of worlds in which the first sentence is true and the set of worlds in which the second sentence is true.
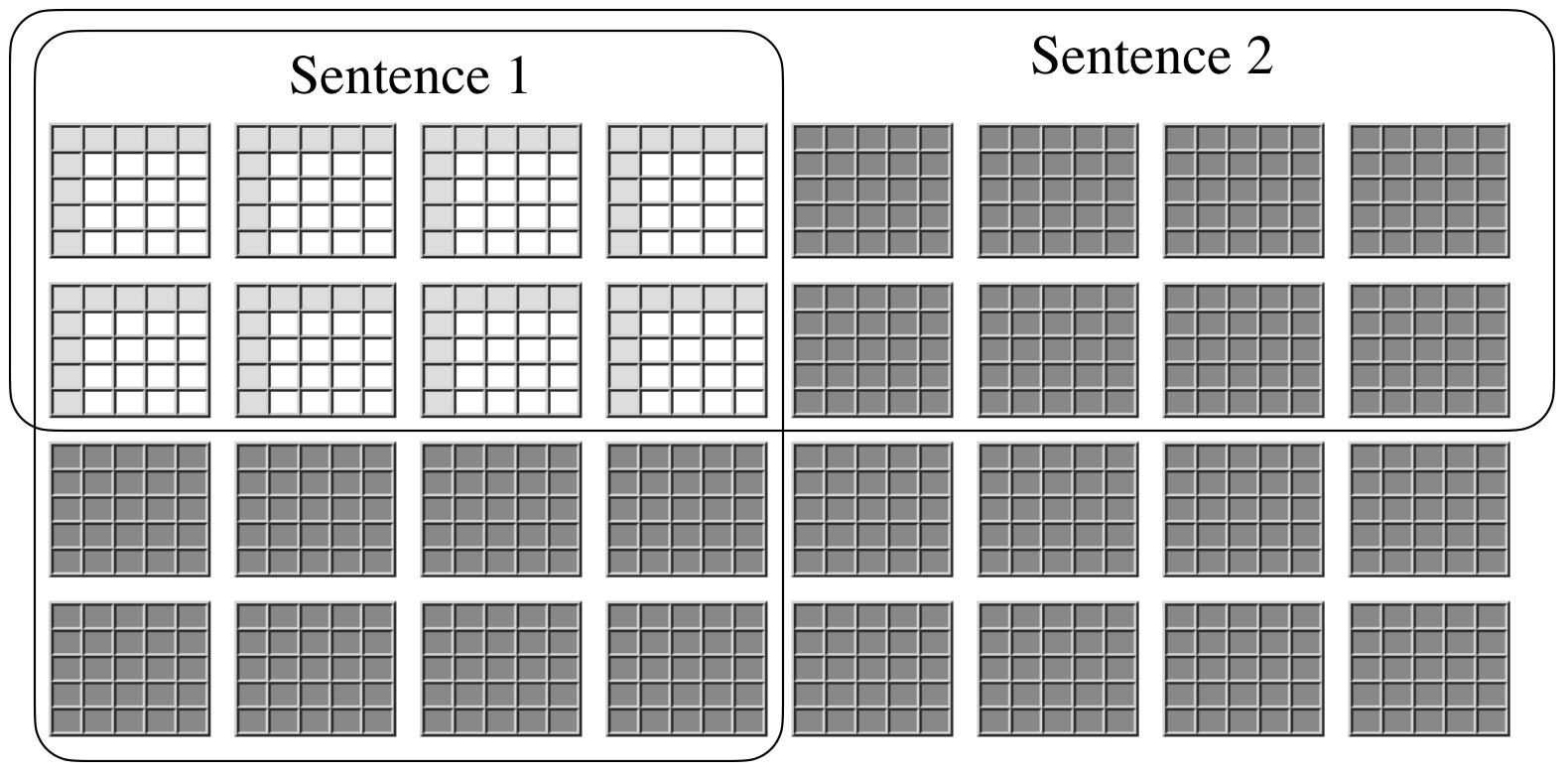
Ideally, when we have enough sentences, we know exactly how things stand.

Effective communication requires a language that allows us to express what we know, no more and no less. If we know the state of the world, then we should write enough sentences to communicate this to others. If we do not know which of various ways the world could be, we need a language that allows us to express only what we know, i.e. which worlds are possible and which are not. The language of Logic gives us a means to express incomplete information when that is all we have and to express complete information when full information is available.
|
|
Once we know which world is correct, we can see that some sentences must be true even though they are not included in the premises we are given. For example, in the first world we saw above, we can see that Bess likes Cody, even though we are not told this fact explicitly. Similarly, we can see that Abby does not like Bess.
Unfortunately, things are not always so simple. Although logical sentences can sometimes pinpoint a specific world from among many possible worlds, this is not always the case. Sometimes, a collection of sentences only partially constrains the world. For example, there are four different worlds that satisfy the sentences in the previous section.
| |
Abby |
Bess |
Cody |
Dana |
| Abby |
|
|
 |
|
| Bess |
|
|
 |
|
| Cody |
 |
 |
|
 |
| Dana |
|
|
 |
|
|
| |
Abby |
Bess |
Cody |
Dana |
| Abby |
|
 |
 |
|
| Bess |
|
|
 |
|
| Cody |
 |
 |
|
 |
| Dana |
|
|
 |
|
|
| |
Abby |
Bess |
Cody |
Dana |
| Abby |
|
|
 |
|
| Bess |
|
|
 |
|
| Cody |
 |
 |
|
 |
| Dana |
|
 |
 |
|
|
| |
Abby |
Bess |
Cody |
Dana |
| Abby |
|
 |
 |
|
| Bess |
|
|
 |
|
| Cody |
 |
 |
|
 |
| Dana |
|
 |
 |
|
|
In situations like this, which world should we use in answering questions? The good news it that sometimes it does not matter. Even though a set of sentences does not determine a unique world, there are some sentences that have the same truth value in every world that satisfies the given sentences, and we can use that value in answering questions.
This is logical entailment. We say that a set of premises logically entails a conclusion if and only if every world that satisfies the premises also satisfies the conclusion.
What can we conclude from the bits of information in our sample logical sentences? Quite a bit, as it turns out. In our example, we see that Bess likes Cody in all four worlds. We also see Bess does not like Abby in all four worlds. Does Dana like Bess? Since there are different values in different worlds, we cannot say yes and we cannot say no. All we can say is Maybe. In the real world, either Dana likes Bess or she doesn't. However, we do not have enough information to say which case is correct.
Model checking is the process of examining the set of all worlds to determine logical entailment. To check whether a set of sentences logically entails a conclusion, we use our premises to determine which worlds are possible and then examine those worlds to see whether or not they satisfy our conclusion. If the number of worlds is not too large, this method works well.
Unfortunately, in general, there are many, many possible worlds; and, in some cases, the number of possible worlds is infinite, in which case model checking is impossible. So what do we do? The answer is logical reasoning and logical proofs.
|
|
Logical proofs are analogous to derivations in algebra. We can try solving algebraic equations by randomly trying different values for the variables in those equations. However, we can usually get to an answer faster by manipulating our equations syntactically. Logical reasoning is similar. Rather than checking all worlds, we simply apply syntactic operations to the premises we are given to generate conclusions.
One of Aristotle's great contributions to philosophy was the identification of syntactic operations of this sort. Such operations are typically called rules of inference. By applying rules of inference to premises, we produce conclusions that are entailed by those premises. A proof is a sequence of such rule applications. We can think of individual reasoning steps as the atoms out of which proof molecules are built.
As an example of a rule of inference, consider the reasoning step shown below. We know that all Accords are Hondas, and we know that all Hondas are Japanese cars. Consequently, we can conclude that all Accords are Japanese cars.
| All Accords are Hondas. |
| All Hondas are Japanese. |
| Therefore, all Accords are Japanese. |
Now consider another example. We know that all borogoves are slithy toves, and we know that all slithy toves are mimsy. Consequently, we can conclude that all borogoves are mimsy. What's more, in order to reach this conclusion, we do not need to know anything about borogoves or slithy toves or what it means to be mimsy.
All borogoves are slithy toves.
All slithy toves are mimsy.
Therefore, all borogoves are mimsy.
|
What is interesting about these examples is that they share the same reasoning structure, viz. the pattern shown below.
All x are y.
All y are z.
Therefore, all x are z.
|
Two things are worthy of note here. First of all, correctness in logical reasoning is determined by the logical operators in our sentences, not the objects and relationships mentioned in those sentences. Second, the conclusion is guaranteed to be true only if the premises are true.
The philosopher Bertrand Russell summed this situation up as follows. Logic may be defined as the subject in which we never know what we are talking about nor whether what we are saying is true. We do not need to know anything about the concepts in our premises except for the information expressed in those premises. Furthermore, while our conclusion must be true if our premises are true, it can be false if one or more of our premises is false.
The existence of reasoning patterns is fundamental in Logic but raises important questions. Which rules of inference are correct? Are there many such patterns or just a few?
Let us consider the first of these questions. Obviously, there are patterns that are just plain wrong in the sense that they can lead to incorrect conclusions. Consider, as an example, the faulty reasoning pattern shown below.
All x are y.
Some y are z.
Therefore, some x are z.
|
Now let us take a look at an instance of this pattern. If we replace x by Toyotas and y by cars and z by made in America, we get the following line of argument, leading to a conclusion that happens to be correct.
All Toyotas are cars.
Some cars are made in America.
Therefore, some Toyotas are made in America.
|
On the other hand, if we replace x by Toyotas and y by cars and z by Porsches, we get a line of argument leading to a conclusion that is questionable.
All Toyotas are cars.
Some cars are Porsches.
Therefore, some Toyotas are Porsches.
|
What distinguishes a correct pattern from one that is incorrect is that it must always lead to correct conclusions, i.e. they must be correct so long as the premises on which they are based are correct. As we will see, this is the defining criterion for what we call deduction.
Now, it is noteworthy that there are patterns of reasoning that are not always correct but are sometimes useful. There is induction, abduction, analogy, and so forth.
Induction is reasoning from the particular to the general. The example shown below illustrates this. In this case, the induction is incomplete. Although we have seen many ravens, we have not seen them all. However, if we see enough cases in which something is true and we never see a case in which it is false, we tend to conclude that it is always true. Unfortunately, when induction is incomplete, as in this case, it is not sound. There might be an albino raven that we have not yet seen.
I have seen 1000 black ravens.
I have never seen a raven that is not black.
Therefore, every raven is black.
Now try red Hondas.
|
Incomplete induction is the basis for Science (and machine learning). Deduction is the subject matter of Logic. Science aspires to discover / propose new knowledge. Logic aspires to apply and/or analyze existing knowledge.
This distinction was at the heart of a famous disagreement between the physicist Albert Einstein and his contemporary Niels Bohr in which Bohr derided Einstein's emphasis on deduction rather than induction. He reputedly told Einstein: You are not thinking; you are just being logical. Bohr was a fan of induction and thought that Einstein placed too much emphasis on deduction.
Of all types of reasoning, deduction is the only one that guarantees its conclusions in all cases, it produces only those conclusions that are logically entailed by one's premises.
In talking about Logic, we now have two notions - logical entailment and provability. A set of premises logically entails a conclusion if and only if every possible world that satisfies the premises also satisfies the conclusion. A sentence is provable from a set of premises if and only if there is a finite sequence of sentences in which every element is either a premise or the result of applying a deductive rule of inference to earlier members in the sequence.
These concepts are quite different. One is based on possible worlds; the other is based on symbolic manipulation of expressions. Yet, for "well-behaved" logics, it turns out that logical entailment and provability are identical - a set of premises logically entails a conclusion if and only if the conclusion is provable from the premises. Even if the number of worlds is infinite, it is possible in such logics to produce a finite proof of the conclusion, i.e. we can determine logical entailment without going through all possible worlds. This is a very big deal.
|
|
So far, we have illustrated everything with sentences in English. While natural language works well in many circumstances, it is not without its problems. Natural language sentences can be complex; they can be ambiguous; and failing to understand the meaning of a sentence can lead to errors in reasoning.
As an example of ambiguity, suppose I were to write the sentence There's a girl in the room with a telescope. See the following figure for two possible meanings of this sentence. Am I saying that there is a girl in a room containing a telescope? Or am I saying that there is a girl in the room and she is holding a telescope?

Such complexities and ambiguities can sometimes be humorous if they lead to interpretations the author did not intend. See the examples below for some infamous newspaper headlines with multiple interpretations. Using a formal language eliminates such unintentional ambiguities (and, for better or worse, avoids any unintentional humor as well).
| Crowds Rushing to See Pope Trample 6 to Death |
| Journal Star, Peoria, 1980 |
|
|
| Scientists Grow Frog Eyes and Ears |
British Left Waffles On Falkland Islands |
| The Daily Camera, Boulder, 2000 |
|
|
|
| Food Stamp Recipients Turn to Plastic |
Indian Ocean Talks |
| The Miami Herald, 1991 |
The Plain Dealer, 1977 |
|
|
| Fried Chicken Cooked in Microwave Wins Trip |
| The Oregonian, Portland, 1981 |
|
As an illustration of errors that arise in reasoning with sentences in natural language, consider the following examples. In the first, we use the transitivity of the better relation to derive a conclusion about the relative quality of champagne and soda from the relative quality of champagne and beer and the relative quality of beer and soda. So far so good.
| Champagne is better than beer. |
| Beer is better than soda. |
| Therefore, champagne is better than soda. |
This makes sense. It is an example of a general rule about the transitivity of the better relation. If x is better than y and y is better than z, then x better than z.
| x is better than y. |
| y is better than z. |
| Therefore, x is better than z. |
Now, consider what happens when we apply this rule in the case illustrated below. Bad sex is better than nothing. Nothing is better than good sex. Therefore, bad sex is better than good sex. Really?
| Bad sex is better than nothing. |
| Nothing is better than good sex. |
| Therefore, bad sex is better than good sex. |
The form of the argument is the same as in the previous example, but the conclusion is somewhat less believable. The problem in this case is that the use of nothing here is syntactically similar to the use of beer in the preceding example, but in English it means something entirely different.
Logic eliminates these difficulties through the use of a formal language for encoding information. Given the syntax and semantics of this formal language, we can give a precise definition for the notion of logical conclusion. Moreover, we can establish precise reasoning rules that produce all and only logical conclusions.
In this regard, there is a strong analogy between the methods of Formal Logic and those of high school algebra. To illustrate this analogy, consider the following algebra problem.
Xavier is three times as old as Yolanda. Xavier's age and Yolanda's age add up to twelve. How old are Xavier and Yolanda?
Typically, the first step in solving such a problem is to express the information in the form of equations. If we let x represent the age of Xavier and y represent the age of Yolanda, we can capture the essential information of the problem as shown below.
Using the methods of algebra, we can then manipulate these expressions to solve the problem. First we subtract the second equation from the first.
| x - 3y = 0 |
| x + y = 12 |
|
| -4y = -12 |
Next, we divide each side of the resulting equation by -4 to get a value for y. Then substituting back into one of the preceding equations, we get a value for x.
Now, consider the following logic problem.
If Mary loves Pat, then Mary loves Quincy. If it is Monday and raining, then Mary loves Pat or Quincy. If it is Monday and raining, does Mary love Quincy?
As with the algebra problem, the first step is formalization. Let p represent the possibility that Mary loves Pat; let q represent the possibility that Mary loves Quincy; let m represent the possibility that it is Monday; and let r represent the possibility that it is raining.
With these abbreviations, we can represent the essential information of this problem with the following logical sentences. The first says that p implies q, i.e. if Mary loves Pat, then Mary loves Quincy. The second says that m and r implies p or q, i.e. if it is Monday and raining, then Mary loves Pat or Mary loves Quincy.
As with Algebra, Formal Logic defines certain operations that we can use to manipulate expressions. The operation shown below is a variant of what is called Propositional Resolution. The expressions above the line are the premises of the rule, and the expression below is the conclusion.
| p1 ∧ ... ∧ pk |
⇒ |
q1 ∨ ... ∨ ql |
| r1 ∧ ... ∧ rm |
⇒ |
s1 ∨ ... ∨ sn |
|
| p1 ∧ ... ∧ pk ∧ r1 ∧ ... ∧ rm |
⇒ |
q1 ∨ ... ∨ ql ∨ s1 ∨ ... ∨ sn |
There are two elaborations of this operation. (1) If a proposition on the left hand side of one sentence is the same as a proposition on the right hand side of the other sentence, it is okay to drop the two symbols, with the proviso that only one such pair may be dropped. (2) If a constant is repeated on the same side of a single sentence, all but one of the occurrences can be deleted.
We can use this operation to solve the problem of Mary's love life. Looking at the two premises above, we notice that p occurs on the left-hand side of one sentence and the right-hand side of the other. Consequently, we can cancel the p and thereby derive the conclusion that, if is Monday and raining, then Mary loves Quincy or Mary loves Quincy.
| p | ⇒ | q |
| m ∧ r | ⇒ | p ∨ q |
|
| m ∧ r | ⇒ | q ∨ q |
Dropping the repeated symbol on the right hand side, we arrive at the conclusion that, if it is Monday and raining, then Mary loves Quincy.
This example is interesting in that it showcases our formal language for encoding logical information. As with algebra, we use symbols to represent relevant aspects of the world in question, and we use operators to connect these symbols in order to express information about the things those symbols represent.
The example also introduces one of the most important operations in Formal Logic, viz. Resolution (in this case a restricted form of Resolution). Resolution has the property of being complete for an important class of logic problems, i.e. it is the only operation necessary to solve any problem in the class.
|
|
The existence of a formal language for representing information and the existence of a corresponding set of mechanical manipulation rules together have an important consequence, viz. the possibility of automated reasoning using digital computers.
The idea is simple. We use our formal representation to encode the premises of a problem as data structures in a computer, and we program the computer to apply our mechanical rules in a systematic way. The rules are applied until the desired conclusion is attained or until it is determined that the desired conclusion cannot be attained. (Unfortunately, in some cases, this determination cannot be made; and the procedure never halts. Nevertheless, as discussed in later chapters, the idea is basically sound.)
Although the prospect of automated reasoning has achieved practical realization only in the last few decades, it is interesting to note that the concept itself is not new. In fact, the idea of building machines capable of logical reasoning has a long tradition.
One of the first individuals to give voice to this idea was Leibnitz. He conceived of "a universal algebra by which all knowledge, including moral and metaphysical truths, can some day be brought within a single deductive system". Having already perfected a mechanical calculator for arithmetic, he argued that, with this universal algebra, it would be possible to build a machine capable of rendering the consequences of such a system mechanically.
Boole gave substance to this dream in the 1800s with the invention of Boolean algebra and with the creation of a machine capable of computing accordingly.
The early twentieth century brought additional advances in Logic, notably the invention of the predicate calculus by Russell and Whitehead and the proof of the corresponding completeness and incompleteness theorems by Godel in the 1930s.
The advent of the digital computer in the 1940s gave increased attention to the prospects for automated reasoning. Research in artificial intelligence led to the development of efficient algorithms for logical reasoning, highlighted by Robinson's invention of resolution theorem proving in the 1960s.
Today, the prospect of automated reasoning has moved from the realm of possibility to that of practicality, with the creation of logic technology in the form of automated reasoning systems, such as Vampire, Prover9, the Prolog Technology Theorem Prover, and others.
The emergence of this technology has led to the application of logic technology in a wide variety of areas. The following paragraphs outline some of these uses.
Mathematics. Automated reasoning programs can be used to check proofs and, in some cases, to produce proofs or portions of proofs.
Engineering. Engineers can use the language of Logic to write specifications for their products and to encode their designs. Automated reasoning tools can be used to simulate designs and in some cases validate that these designs meet their specification. Such tools can also be used to diagnose failures and to develop testing programs.
Database Systems. By conceptualizing database tables as sets of simple sentences, it is possible to use Logic in support of database systems. For example, the language of Logic can be used to define virtual views of data in terms of explicitly stored tables, and it can be used to encode constraints on databases. Automated reasoning techniques can be used to compute new tables, to detect problems, and to optimize queries.
Data Integration The language of Logic can be used to relate the vocabulary and structure of disparate data sources, and automated reasoning techniques can be used to integrate the data in these sources.
Logical Spreadsheets. Logical spreadsheets generalize traditional spreadsheets to include logical constraints as well as traditional arithmetic formulas. Examples of such constraints abound. For example, in scheduling applications, we might have timing constraints or restrictions on who can reserve which rooms. In the domain of travel reservations, we might have constraints on adults and infants. In academic program sheets, we might have constraints on how many courses of varying types that students must take.
Law and Business. The language of Logic can be used to encode regulations and business rules, and automated reasoning techniques can be used to analyze such regulations for inconsistency and overlap.
|
|
Although Logic is a single field of study, there is more than one logic in this field. In the three main units of this book, we look at three different types of logic, each more sophisticated than the one before.
Propositional Logic is the logic of propositions. Symbols in the language represent "conditions" in the world, and complex sentences in the language express interrelationships among these conditions. The primary operators are Boolean connectives, such as and, or, and not.
Relational Logic expands upon Propositional Logic by providing a means for explicitly talking about individual objects and their interrelationships (not just monolithic conditions). In order to do so, we expand our language to include object constants and relation constants, variables and quantifiers.
Functional Logic takes us one step further by providing a means for describing worlds with infinitely many objects. The resulting logic is much more powerful than Propositional Logic and Relational Logic. Unfortunately, as we shall see, some of the nice computational properties of the first two logics are lost as a result.
Each logic introduces new issues and capabilities. Despite their differences, there are many commonalities among these logics. In particular, in each case, there is a language with a formal syntax and a precise semantics; there is a notion of logical entailment; and there are legal rules for manipulating expressions in the language.
These similarities allow us to compare the logics and to gain an appreciation of the fundamental tradeoff between expressiveness and computational complexity. On the one hand, the introduction of additional linguistic complexity makes it possible to say things that cannot be said in more restricted languages. On the other hand, the introduction of additional linguistic flexibility has adverse effects on computability. As we proceed though the material, our attention will range from the completely computable case of Propositional Logic to a variant that is not at all computable.
There are also some topics that are relevant to Logic but are out of scope for this course, such as probability, metaknowledge (knowledge about knowledge), and paradoxes (e.g. This sentence is false.). Also, negation as failure (knowing not versus not knowing, non-deductive reasoning methods (like induction), and paraconsistent reasoning (i.e. reasoning from inconsistent premises). We touch on these extensions in this course, but we do not talk about them in any depth.
One final comment. In the hopes of preventing difficulties, it is worth pointing out a potential source of confusion. This book exists in the meta world. It contains sentences about sentences; it contains proofs about proofs. In some places, we use similar mathematical symbology both for sentences in Logic and sentences about Logic. Wherever possible, we try to be clear about this distinction, but the potential for confusion remains. Unfortunately, this comes with the territory. We are using Logic to study Logic. It is our most powerful intellectual tool.
|
Use the arrow keys to navigate.
Press the escape key to toggle all / one.
|
|
